geomshadertut1

Two months ago was introduced the G80 and the set of OpenGL extensions allowing access to all of its new functionalities (cf. my posts on G80 architecture and OpenGL extensions, it is in French but can be translated with the British flag button on top left. You can also refer to http://www.g-truc.net/ that also provides a good analysis on G80 OpenGL extensions in french). Among them are GPU Shaders model 4 and the new Geometry Shader they introduce.

For the first time, on-GPU dynamic generation of geometric primitives becomes possible.  But till now, very few examples and tutorials on theses functionalities are available. The only tutorial I have been able to find is the one from Xie Yongming, it’s a good start but unfortunately its source code is unavailable.

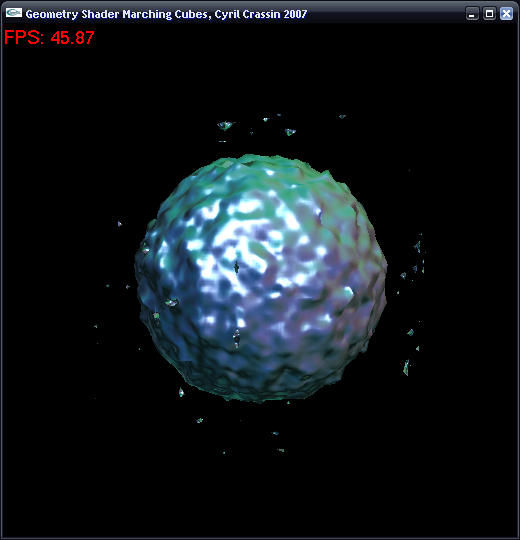
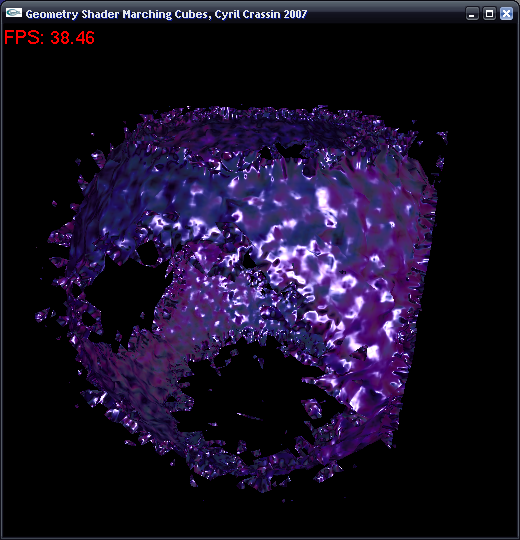
This simple example will show how to use GLSL Geometry Shaders (EXT_geometry_shader4 and EXT_gpu_shader4) and the new integer texture formats (EXT_texture_integer) extensions to implement the Marching Cubes algorithm entirely on the GPU. The implementation I will present is probably not the most efficient but I think it is a good example, showing the usage of the new shader stage, new texture formats and binary operations within shader.

Generalities

    Geometry Shader stage take place between Vertex Shader and Viewport Clipping stage. It operates on assembled primitives transformed by Vertex Shader (Points, Lines or Triangles) and generates -per primitive- a set of new primitives (whose types are currently limited to Points, Line Strip and Triangle Strip) that are assembled in another assembly stage before being sent to Clipping stage and rasterization. All input primitive vertices can be accessed by the program and an arbitrary number of output primitives can be generated, it can also generate no primitive. New primitives types are provided allowing to pass primitives adjacencies informations to the shader.

The first and immediate application of this stage is for implicit surface determination from scalar field and I will show a first approach to implement Marching Cubes algorithm entirely on a Geometry Shader. I am currently making performances benchmarks and optimizations but it already seems to be quite efficient compared to classical CPU implementations.

This implementation is based on Paul Bourke Marching Cubes implementation that can be found at http://local.wasp.uwa.edu.au/~pbourke/geometry/polygonise/ . This code use two tables helping to find quickly edges where vertices should be created and the triangulation of theses vertices for a marching cube grid element.

The idea of the algorithm is to send points primitives to the Geometry Shader, each point representing one Marching Cube grid cell. The Geometry Shader Operate on each point and generate for a point the set of triangles needed to cut the cell with isosurface. 3D scalar field values are fetched from a 16 bits floating point 3D texture and the two accelerations tabs are fetched with integer access to 2D integer textures.

Till the next revision of Cg (certainly 1.6 which is the revision reported by driver’s GLSL compiler), GLSL is the only high level language to allow programming the Geometry Shader Stage. This tutorial will highlight interesting code portions and the full source code is available in the next section.

Source Code and Demo

    The following zip file contain all the C++ source code of this tutorial, a visual studio 8 project and a Windows executable (to use only with a GeForce 8800 or with G80 emulation enabled). It uses GLUT (for Windows: http://www.xmission.com/~nate/glut.html ) for window management and the last version of the GLEW extension loader library (http://glew.sourceforge.net/ ).

You can use key ‘a’ to toggle animation, ‘w’ to switch with wireframe mode, ‘d’ to switch between various data fields, ‘+’/’-‘ or right click drag to change current isolevel and left click drag to rotate around the scene. The ‘m’ key allow to switch between standard geometry shader mode, performance mode (without expensive lighting computation) and software mode for performances comparisons (note this is an highly NOT optimized software code, it is just present to get an IDEA of software performances). The ‘s’ key allow to switch off Swizzled march of input primitives to see the impact on performances of non-spatially optimized grid cells marching.

 

geomshadertut3 geomshadertut2b

System Setup

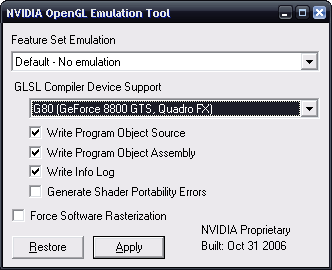
    With current nVidia drivers under Windows (97.44, I didn’t try under Linux), G80 new OpenGL extensions and GLSL compiler new functionalities are not exposed by default. They must be enabled via the NVIDIA OpenGL Emulation Tools by choosing “G80 (GeForce 8800 GTS, Quadro Fx)” into the “GLSL Compiler Device Support” combo box. This tool can also allow to emulate G80 functionalities on older hardwares.

It is also useful for testing and debugging application with software rasterisation. I have indeed been faced with some BSOTD crash, machine freezing and abnormal artifacts during the development of this code certainly due to young drivers and software rasterization mode was useful for preventing this.
emulationtool

 

 

 

OpenGL initialization

    The first step is to create the GLSL Shader program and to load Vertex, Geometry and Fragment Shaders codes from files. The code is not detailed here as it is classical GLSL loading procedure (you will find it in the source code archive). You can notice that a Vertex Shader must be used to be able to use Geometry Shader.

 

//Program object creation
programObject = glCreateProgramObjectARB();
////Shaders loading////
//Geometry Shader loading
initShader("Shaders/TestG80_GS.glsl", GL_GEOMETRY_SHADER_EXT);
//Geometry Shader require a Vertex Shader to be used
initShader("Shaders/TestG80_VS.glsl", GL_VERTEX_SHADER_ARB);
//Fragment Shader for per-fragment lighting
initShader("Shaders/TestG80_FS.glsl", GL_FRAGMENT_SHADER_ARB);
////////

 

Then the Geometry Shader must be setup with input and output primitives types and maximum number of output vertices. This parameter is very important as high values widely impact performances.

//Get max number of geometry shader output vertices
GLint temp;
glGetIntegerv(GL_MAX_GEOMETRY_OUTPUT_VERTICES_EXT,&temp);
std::cout<<"Max GS output vertices:"<<temp<<"\n";

////Setup Geometry Shader////
//Set POINTS primitives as INPUT
glProgramParameteriEXT(programObject,GL_GEOMETRY_INPUT_TYPE_EXT , GL_POINTS );
//Set TRIANGLE STRIP as OUTPUT
glProgramParameteriEXT(programObject,GL_GEOMETRY_OUTPUT_TYPE_EXT , GL_TRIANGLE_STRIP);
//Set maximum number of vertices to be generated by Geometry Shader to 16
//16 is the maximum number of vertices a marching cube configuration can own
//This parameter is very important and have an important impact on Shader performances
//Its value must be chosen closer as possible to real maximum number of vertices
glProgramParameteriEXT(programObject,GL_GEOMETRY_VERTICES_OUT_EXT, 16);

Then the program is linked and validated. After that, textures are generated to store optimization tables that will be used per marching cube (and so per geometry shader) for triangle generation. We will use for that a new integer texture format introduced by the GL_EXT_texture_integer extension. Theses textures allow direct integer fetch within shaders and can be accessed directly with integer address via new texture fetch commands.

 

//Edge Table texture//
//This texture store the 256 different configurations of a marching cube.
//This is a table accessed with a bitfield of the 8 cube edges states
//(edge cut by isosurface or totally in or out).
//(cf. MarchingCubes.cpp)
glGenTextures(1, &(this->edgeTableTex));
glActiveTexture(GL_TEXTURE1);
glEnable(GL_TEXTURE_2D);

glBindTexture(GL_TEXTURE_2D, this->edgeTableTex);
//Integer textures must use nearest filtering mode
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

//We create an integer texture with new GL_EXT_texture_integer formats
glTexImage2D( GL_TEXTURE_2D, 0, GL_ALPHA16I_EXT, 256, 1, 0,
GL_ALPHA_INTEGER_EXT, GL_INT, &edgeTable);

//Triangle Table texture//
//This texture store the vertex index list for
//generating the triangles of each configurations.
//(cf. MarchingCubes.cpp)
glGenTextures(1, &(this->triTableTex));
glActiveTexture(GL_TEXTURE2);
glEnable(GL_TEXTURE_2D);

glBindTexture(GL_TEXTURE_2D, this->triTableTex);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

glTexImage2D( GL_TEXTURE_2D, 0, GL_ALPHA16I_EXT, 16, 256, 0,
GL_ALPHA_INTEGER_EXT, GL_INT, &triTable);

Volume data are simply a distance field generated manually for this example but could be any scalar field.

//Datafield//
//Store the volume data to polygonise
glGenTextures(1, &(this->dataFieldTex));

glActiveTexture(GL_TEXTURE0);
glEnable(GL_TEXTURE_3D);
glBindTexture(GL_TEXTURE_3D, this->dataFieldTex);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_3D, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

//Generate a distance field to the center of the cube
dataField=new float[128*128*128];
for(int k=0; k<128; k++)
for(int j=0; j<128; j++)
for(int i=0; i<128; i++){
dataField[i+j*128+k*128*128]=Vector3f(i, j, k).distance(Vector3f(64,64,64))/64.0f;
}

glTexImage3D( GL_TEXTURE_3D, 0, GL_ALPHA32F_ARB, 128, 128, 128, 0,
GL_ALPHA, GL_FLOAT, dataField);
delete [] dataField;
dataField=NULL;

The final initialization step is to assign uniforms attributes to the shaders. We precompute the x, y and z decal associated with each vertex of a marching cube allowing to get their position in the Geometry Shader.

////Samplers assignment///
glUniform1iARB(glGetUniformLocationARB(programObject, "dataFieldTex"), 0);
glUniform1iARB(glGetUniformLocationARB(programObject, "edgeTableTex"), 1);
glUniform1iARB(glGetUniformLocationARB(programObject, "triTableTex"), 2);

////Uniforms parameters////
//Initial isolevel
glUniform1fARB(glGetUniformLocationARB(programObject, "isolevel"), isolevel);
//Step in data 3D texture for gradient computation (lighting)
glUniform3fARB(glGetUniformLocationARB(programObject, "dataStep"),
cubeStep.x, cubeStep.y, cubeStep.z);

//Decal for each vertex in a marching cube
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[0]"),
0.0f, 0.0f, 0.0f);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[1]"),
cubeStep.x, 0.0f, 0.0f);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[2]"),
cubeStep.x, cubeStep.y, 0.0f);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[3]"),
0.0f, cubeStep.y, 0.0f);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[4]"),
0.0f, 0.0f, cubeStep.z);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[5]"),
cubeStep.x, 0.0f, cubeStep.z);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[6]"),
cubeStep.x, cubeStep.y, cubeStep.z);
glUniform3fARB(glGetUniformLocationARB(programObject, "vertDecals[7]"),
0.0f, cubeStep.y, cubeStep.z);

 

OpenGL Rendering loop

The rendering loop only send one vertex per marching cube of the marching cubes grid as points. Theses points are passed through and kept “as is” by the Vertex Shader. Then the Geometry Shader is called for each point and generate the triangles for the the marching cube grid element associated with this point.

Theses triangles are then rasterized and a Fragment Shader lit them.

 

Geometry Shader GLSL Code

//GLSL version 1.20
#version 120
//New G80 extensions
#extension GL_EXT_geometry_shader4 : enable
#extension GL_EXT_gpu_shader4 : enable

//Volume data field texture
uniform sampler3D dataFieldTex;
//Edge table texture
uniform isampler2D edgeTableTex;
//Triangles table texture
uniform isampler2D triTableTex;
//Global iso level
uniform float isolevel;
//Marching cubes vertices decal
uniform vec3 vertDecals[8];
//Vertices position for fragment shader
varying vec4 position;

//Get vertex i position within current marching cube
vec3 cubePos(int i){
return gl_PositionIn[0].xyz + vertDecals[i];
}

//Get vertex i value within current marching cube
float cubeVal(int i){
return texture3D(dataFieldTex, (cubePos(i)+1.0f)/2.0f).a;
}

//Get triangle table value
int triTableValue(int i, int j){
return texelFetch2D(triTableTex, ivec2(j, i), 0).a;
}

//Compute interpolated vertex along an edge
vec3 vertexInterp(float isolevel, vec3 v0, float l0, vec3 v1, float l1){
return mix(v0, v1, (isolevel-l0)/(l1-l0));
}

//Geometry Shader entry point
void main(void) {
int cubeindex=0;
float cubeVal0 = cubeVal(0);
float cubeVal1 = cubeVal(1);
float cubeVal2 = cubeVal(2);
float cubeVal3 = cubeVal(3);
float cubeVal4 = cubeVal(4);
float cubeVal5 = cubeVal(5);
float cubeVal6 = cubeVal(6);
float cubeVal7 = cubeVal(7);

//Determine the index into the edge table which
//tells us which vertices are inside of the surface
cubeindex = int(cubeVal0 < isolevel);
cubeindex += int(cubeVal1 < isolevel)*2;
cubeindex += int(cubeVal2 < isolevel)*4;
cubeindex += int(cubeVal3 < isolevel)*8;
cubeindex += int(cubeVal4 < isolevel)*16;
cubeindex += int(cubeVal5 < isolevel)*32;
cubeindex += int(cubeVal6 < isolevel)*64;
cubeindex += int(cubeVal7 < isolevel)*128;

//Cube is entirely in/out of the surface
if (cubeindex ==0 || cubeindex == 255)
return;

vec3 vertlist[12];
//Find the vertices where the surface intersects the cube
vertlist[0] = vertexInterp(isolevel, cubePos(0), cubeVal0, cubePos(1), cubeVal1);
vertlist[1] = vertexInterp(isolevel, cubePos(1), cubeVal1, cubePos(2), cubeVal2);
vertlist[2] = vertexInterp(isolevel, cubePos(2), cubeVal2, cubePos(3), cubeVal3);
vertlist[3] = vertexInterp(isolevel, cubePos(3), cubeVal3, cubePos(0), cubeVal0);
vertlist[4] = vertexInterp(isolevel, cubePos(4), cubeVal4, cubePos(5), cubeVal5);
vertlist[5] = vertexInterp(isolevel, cubePos(5), cubeVal5, cubePos(6), cubeVal6);
vertlist[6] = vertexInterp(isolevel, cubePos(6), cubeVal6, cubePos(7), cubeVal7);
vertlist[7] = vertexInterp(isolevel, cubePos(7), cubeVal7, cubePos(4), cubeVal4);
vertlist[8] = vertexInterp(isolevel, cubePos(0), cubeVal0, cubePos(4), cubeVal4);
vertlist[9] = vertexInterp(isolevel, cubePos(1), cubeVal1, cubePos(5), cubeVal5);
vertlist[10] = vertexInterp(isolevel, cubePos(2), cubeVal2, cubePos(6), cubeVal6);
vertlist[11] = vertexInterp(isolevel, cubePos(3), cubeVal3, cubePos(7), cubeVal7);

// Create the triangle
gl_FrontColor=vec4(cos(isolevel*5.0-0.5), sin(isolevel*5.0-0.5), 0.5, 1.0);
int i=0;
//Strange bug with this way, uncomment to test
//for (i=0; triTableValue(cubeindex, i)!=-1; i+=3) {
while(true){
if(triTableValue(cubeindex, i)!=-1){
//Generate first vertex of triangle//
//Fill position varying attribute for fragment shader
position= vec4(vertlist[triTableValue(cubeindex, i)], 1);
//Fill gl_Position attribute for vertex raster space position
gl_Position = gl_ModelViewProjectionMatrix* position;
EmitVertex();
//Generate second vertex of triangle//
//Fill position varying attribute for fragment shader
position= vec4(vertlist[triTableValue(cubeindex, i+1)], 1);
//Fill gl_Position attribute for vertex raster space position
gl_Position = gl_ModelViewProjectionMatrix* position;
EmitVertex();
//Generate last vertex of triangle//
//Fill position varying attribute for fragment shader
position= vec4(vertlist[triTableValue(cubeindex, i+2)], 1);
//Fill gl_Position attribute for vertex raster space position
gl_Position = gl_ModelViewProjectionMatrix* position;
EmitVertex();
//End triangle strip at firts triangle
EndPrimitive();
}else{
break;
}
i=i+3; //Comment it for testing the strange bug
}
}

Performances

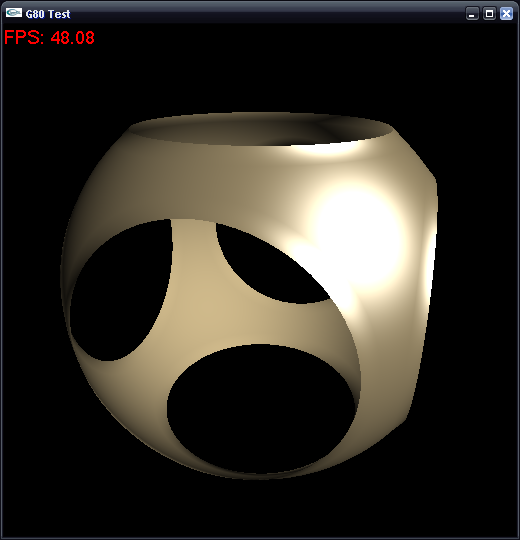
As I said in introduction, the code I have posted here is not optimized at all and is for example purpose only. The archive file I provide contain a more optimized version of this source code enhanced with the help of Jan Vlietinck (you can visit his webpage: http://users.belgacom.net/gc610902/ ) I would like to thanks a lot for it’s help. With this new code, we can achieve very interesting performances on iso-surface extraction.

For instance, framerates from 220 to 500FPS (depending on the number of triangles generated) are achieves on 128^3 data with 32^3 marching cubes grid on a GeForce 8800GTS. On a 64^3 marching cubes grid, I obtained 44 to 77 FPS on the same data and configuration. To compare, I have implemented a simple software marching cubes that can achieves approximatively 53FPS (32^3) and 7FPS (34^3) on the same tests on my Athlon 64 3400+.

But this code is not optimized at all and I don’t think it can be used as a realistic reference of software codes performances, it just help to get an idea. At this subject if anybody have a good and highly optimized software marching cubes implementation I would be interested…

More details on theses optimizations and last version of the code to come soon…

Contacts and feedbacks

Any commentaries, feedbacks and questions on this code and tutorial are welcome and can be done sending me an E-MAIL (cyril AT icare3d.org) or letting a commentary bellow. I hope this mini-tutorial will be useful.

References

    – NVidia G80 Extensions reference: http://developer.nvidia.com/object/nvidia_opengl_specs.html

    – Xie Yongming tutorial: http://appsrv.cse.cuhk.edu.hk/~ymxie/Geometry_Shader/

    – Paul Bourke Marching Cubes Tutorial: http://local.wasp.uwa.edu.au/~pbourke/geometry/polygonise/

– Original Lorensen and Cline Article for SIGGRAPH 87: http://www.cs.duke.edu/education/courses/fall01/cps124/resources/p163-lorensen.pdf